A correlation is a statistical measure that shows the relationship between two variables. It measures how much a change in one variable is linked to a change in another. A positive correlation means that as one variable increases, the other also increases, while a negative correlation means that as one variable increases, the other decreases. The range of the correlation coefficient, represented by r, is -1 to 1. An r value of 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation between the variables.
The Pearson correlation coefficient is a widely used measure of correlation calculated using the covariance of the variables divided by the product of their standard deviations. Correlation can reveal important relationships in data, assisting in predictions and understanding variable interdependencies. For example, in finance, correlation can help assess how different assets move in relation to each other. However, correlation does not imply causation or that one variable causes changes in another.
While a high correlation might suggest a relationship worth investigating further, additional analysis is required to determine causality. Scatter plots are often used to visually assess the correlation between two variables. In practice, correlations are used in fields like economics, psychology, biology, and engineering. Understanding correlation is important for data analysis, decision-making, and model building. It is a foundational concept in statistics and data science. Misinterpreting correlation can lead to erroneous conclusions, so it’s crucial to analyze the data contextually.
How many types of correlation exist?
There are three main types of correlation:
Positive Correlation: When two variables move in the same direction, there is a positive correlation. Both variables rise in tandem with an increase in one. For instance, sales of ice cream typically rise in response to rising temperatures, suggesting a positive association. A perfect positive correlation is represented by a correlation coefficient of +1, which falls between 0 and +1. Although positive correlation does not prove causation, it does point to a relationship that is worthwhile to investigate further.
Negative Correlation
When two variables move against one another, there is a negative correlation. The other variable falls while one rises, and vice versa. For instance, there is frequently a negative relationship between academic achievement and TV viewing hours; grades typically decline as TV viewing hours rise. A perfect negative correlation is represented by a correlation value of -1. The correlation coefficient for a negative correlation falls between -1 and 0. A negative correlation does not necessarily suggest causality; rather, it only shows an inverse association.
No Correlation
When there is no apparent relationship between two variables, there is no correlation. There is no consistent pattern of rise or reduction in the other variable when one changes. For instance, there could not be a relationship between shoe size and the amount of study hours. There is no linear relationship when the correlation coefficient for no correlation is approaching to 0. If there is no correlation, then changes in one variable cannot be predicted by changes in the other.
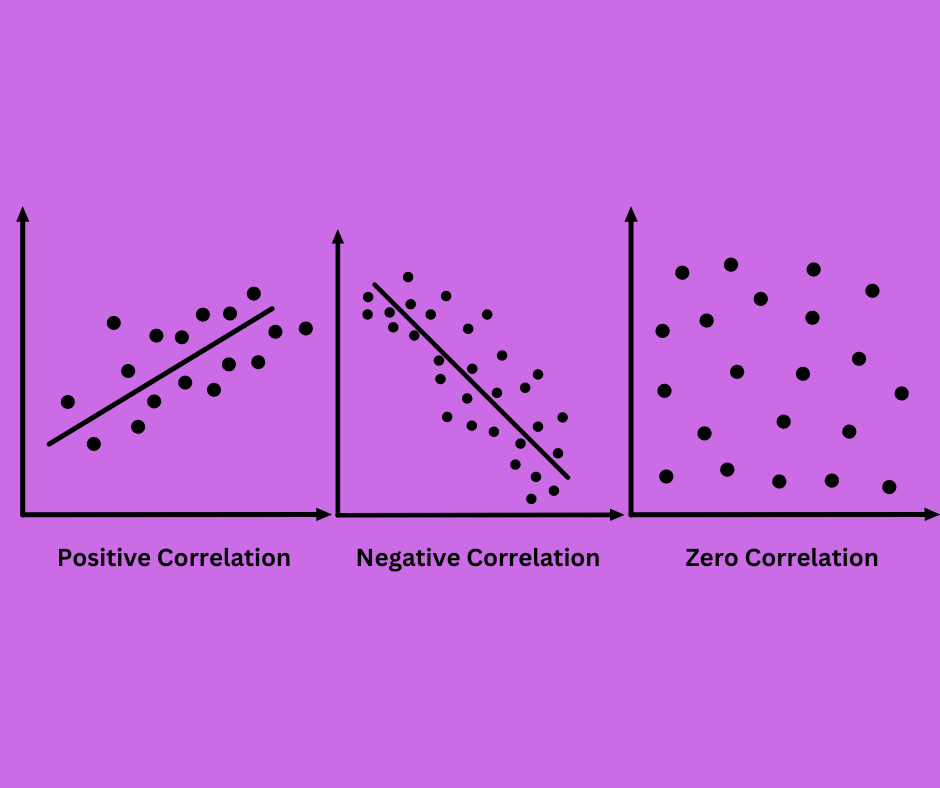
The Correlation value range:
The correlation value, also known as the correlation coefficient, ranges from -1 to 1. Here’s what the values represent:
+1: Perfect positive correlation. As one variable increases, the other variable increases in a perfectly linear relationship.
0: No correlation. The two variables have no linear relationship with one another.
-1: Perfect negative correlation. As one variable increases, the other variable decreases in a perfectly linear relationship.
Interpretation of the Correlation Coefficient:
+0.7 to +1: Strong positive correlation.
+0.3 to +0.7: Moderate positive correlation.
0 to +0.3: Weak positive correlation.
-0.3 to 0: Weak negative correlation.
-0.3 to -0.7: Moderate negative correlation.
-0.7 to -1: Strong negative correlation.
It is important to note that these interpretations can vary slightly depending on the context and field of study. Also, while the correlation coefficient indicates the strength and direction of a linear relationship, it does not imply causation.
There are four primary methods for measuring the correlation between two variables:
1. Pearson Correlation Coefficient:
The linear link between two continuous variables is assessed for both direction and strength using the Pearson correlation coefficient, or “r.” This statement presupposes that the variables have a linear connection and that the data are normally distributed. That is, it evaluates the degree to which the relationship between the variables may be represented by a linear equation. Between -1 and 1, the coefficient 𝑟r denotes a strong positive linear relationship, a strong negative linear relationship, and no linear relationship, with values around 0 indicating no linear relationship. In order to measure the degree of relationship between two continuous variables, one essential statistical tool is the Pearson correlation coefficient.
2. Spearman’s Rank Correlation Coefficient:
The direction and strength of the monotonic link between two ranked variables are determined by the Spearman’s rank correlation coefficient, which is represented by the symbols ρ ρ or 𝑟 𝑠r s. Spearman’s correlation does not rely on a normal distribution of the data or a linear relationship between the variables, in contrast to the Pearson correlation coefficient. Rather, it assesses how well a monotonic function—that is, a function that either continuously increases or decreases—can be used to characterize the connection between the variables. Because of this, Spearman’s correlation is especially helpful when examining ordinal data or non-linear connections. Spearman’s correlation gives information about the direction and strength of associations that may not be seen by linear approaches by comparing the ranks of the data points instead of their actual values.
3. Kendall’s Tau:
Kendall’s Tau, represented by \( \tau \), is a statistic that, based on data ranks, indicates the direction and strength of a relationship between two variables. Kendall’s Tau does not depend on the data being linear or having a normal distribution, in contrast to Pearson’s correlation coefficient. Due to its non-parametric nature, it can be used in scenarios where these presumptions are not true, such as small sample sizes or a high number of tied ranks in the data. By concentrating on the concordance (agreement in rankings) and discordance (discordance in rankings) between pairs of observations, Kendall’s Tau assesses the similarity in the ordering of observations between two variables. Kendall’s Tau offers a strong, widely accepted measure of connection by taking into account the ranks rather than the actual values of the variables.
4. Point-Biserial Correlation:
The relationship between a binary (dichotomous) variable and a continuous variable is evaluated in terms of both direction and strength using the point-biserial correlation. In essence, it is a Pearson correlation coefficient modification meant for situations in which there is just one binary variable. When comparing test scores across two groups (e.g., pass vs. fail), this method can be used to understand how a continuous variable evolves with regard to a binary condition.
All four correlation methods (Pearson, Spearman, Kendall, and point-biserial) have specific uses and presumptions, making them appropriate for examining different kinds of data and relationships found in diverse research settings and fields of study.
How Correlation Works in Information Science
In the field of information science, correlation is essential for analyzing and understanding data relationships. Here’s how it works in this field:
Data Analysis:
Correlation is used to discover relationships between different data sets. For example, it can be used to analyze user behavior on a website to find patterns between the time spent on pages and the likelihood of making a purchase.
Information Retrieval:
Correlation helps improve search algorithms by identifying relevant documents. For instance, if users who search for “data science” also frequently search for “machine learning,” a search engine can correlate these terms to provide better results.
Recommendation Systems:
Correlation is used to enhance recommendation systems. For example, systems like Netflix or Amazon can suggest movies or products by correlating user preferences and behaviors with those of similar users.
Social Network Analysis:
Correlation analysis can identify influential nodes and connections within social networks. This helps in understanding how information spreads and which nodes are crucial for dissemination.
Natural Language Processing:
In NLP, correlation helps in sentiment analysis, topic modeling, and word associations. For instance, analyze the correlation between words and their context in large text corpora to understand meaning and sentiment.
By leveraging correlation, information scientists can extract valuable insights from data, improve the user experience, and enhance the accuracy and efficiency of information systems.



